.gif)
.gif)
| ARTÍCULOS | ||
|
||
|
RESUMEN Siguiendo con un artículo anterior, en este se presentan un conjunto de distribuciones, discretas y continuas, que se encuentran en distintos ambitos del análisis de datos y que, a través de Internet y a través del programa STATLETS, puede obtenerse el cálculo de probabilidades para valores bajo estas distribuciones. |
||
|
En otro documento (Palmer, Jiménez y Rubí, 1999) se introdujeron diferentes formas de obtener, en Internet, las probabilidades asociadas a las distribuciones más comunes en el análisis de datos. A saber: Bernoulli, Binomial y Poisson como distribuciones discretas y las siguientes distribuciones continuas: Normal, t de Student, Ji-cuadrado y F de Snedecor. Este documento introduce un conjunto de distribuciones que asimismo son habituales en el proceso de modelización actual. Así, por ejemplo, el conjunto de distribuciones pertenecientes a la familia exponencial, es de uso habitual en metodologías de análisis como en el marco del análisis de la supervivencia. Pero, aún más, desde que Nelder y Wedderburn presentaran, en 1972, el Modelo Lineal Generalizado, las distribuciones pertenecientes a la familia exponencial son más habituales ya que constituyen el prototipo de distribuciones que caracterizan al conjunto de técnicas que tienen cabida bajo este modelo. Otras distribuciones son comunes y habituales en el campo de actuación de disciplinas tales como la economía, la biología, etc. Como ya decíamos en el documento anterior, estar conectados a Internet permite, en estos momentos, disponer de una serie de recursos que hacen ya innecesario el uso de libros de tablas de estadística o el uso de algún programa informático situado en el disco duro de nuestro ordenador. El objetivo de este artículo es dar información, en forma de enlaces, para que cada usuario busque y encuentre la solución a su problema, cuando este problema consista en obtener una probabilidad asociada a cualquiera de las distribuciones aquí mencionadas, sea discreta o continua. A efectos de tener identificadas las distribuciones, discretas y continuas, utilizadas de forma mas frecuente, se proporciona su función de probabilidad (caso discreto) o su función de densidad de probabilidad (caso continuo), con el ánimo de dar un poco de contenido a cada distribución. Por supuesto que si el usuario quiere tener más información sobre alguna de estas distribuciones le recomendamos que acuda a algún texto especializado.
OTRAS DISTRIBUCIONES UTILIZADAS EN ESTADISTICA Distribución Uniforme Discreta Si se tienen n observaciones, la probabilidad de que la variable aleatoria tome el valor xi viene dada por:
Así pues, en esta distribución cada observación
tiene la misma probabilidad de ocurrencia.
En el siguiente gráfico se muestra la función de probabilidad de la distribución Uniforme Discreta con un rango de valores enteros entre 1 y 10. 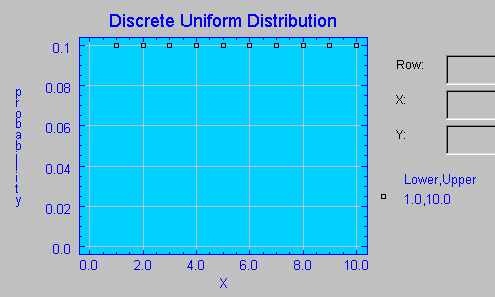
Distribución Binomial Negativa Permite calcular la probabilidad de tener k fracasos antes de que ocurra el r-ésimo éxito.
En el caso de que los sucesos ocurran a intervalos regulares
de tiempo, esta variable proporciona el tiempo total para que
ocurran r éxitos. En el siguiente gráfico se muestra la función de probabilidad de la distribución Binomial negativa con un número de éxitos igual a 10 y una probabilidad de éxito de 0.4. En abcisas se representan los distintos valores que puede tomar la variable X (número de ensayos), y en ordenadas se representa la probabilidad asociada a cada valor posible de X. 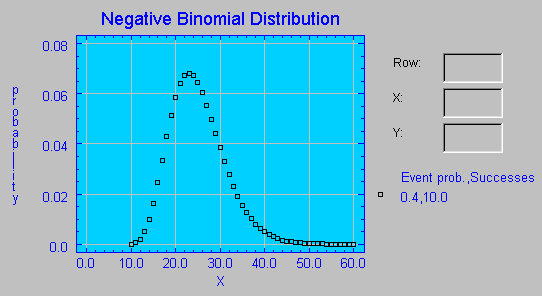
En la dirección http://home.clara.net/sisa/negbino2.htm se puede acceder a una página con la calculadora que se muestra a continuación, en la que se han introducido los parámetros utilizados en el gráfico anterior para el cálculo de probabilidades no acumuladas basadas en la función de probabilidad de la distribución Binomial negativa. S.I.S.A. Simple Interactive Statistical Analysis.  En el calculador anterior se observa cómo la probabilidad de obtener el 10º éxito (probabilidad de éxito de 0.4) en el intento número 30 es de 0.038395. Esta probabilidad obtenida se puede leer de forma aproximada en el gráfico anterior para X=30.
Distribución no acumulada : calculador.UCLA Statistics. Distribución no acumulada: gráfico.UCLA Statistics. Distribución acumulada: calculador. UCLA Statistics. Distribución acumulada: gráfico.UCLA Statistics. Generación
aleatoria de muestras. UCLA Statistics.
Permite calcular la probabilidad de que tengan que realizarse un número k de ensayos para obtener un éxito en el último ensayo, siendo p la probabilidad de obtener un éxito. Así pues, esta distribución es un caso particular de la distribución binomial negativa para el caso en que r=1.
Se utiliza en la distribución de los tiempos de espera, de manera que si los ensayos se realizan a intervalos regulares de tiempo, esta variable aleatoria proporciona el tiempo transcurrido hasta el primer éxito. Por ejemplo, encontrar la primera pieza defectuosa, la primera ocurrencia de un suceso, la llegada de un cliente a un lugar de servicio, la rotura de una cierta pieza, etc. (Aranda y Gómez, 1992). Esta distribución presenta la propiedad denominada propiedad de Markov o de falta de memoria, que implica que la probabilidad de tener que esperar un tiempo ti no depende del tiempo que ya se haya esperado. Hay autores (Aranda y Gómez, 1992).que dicen que a la distribución binomial negativa se la conoce también con el nombre de distribución de Pascal, mientras que otros (Castillo, 1978) definen la distribución de Pascal para el caso de r=1, es decir para la distribución geométrica. En el siguiente gráfico se muestra la función de probabilidad de una distribución Geométrica con una probabilidad de éxito de 0.3. 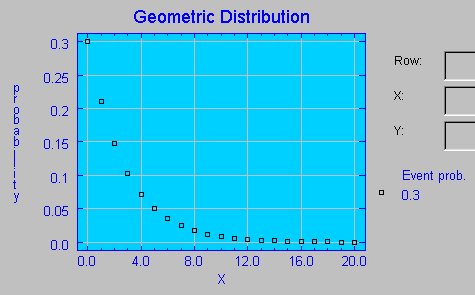 La probabilidad de que se presente un evento determinado (con una probabilidad de éxito de 0.3) en el cuarto intento (X=4) es de 0.072030.
Permite calcular la probabilidad de obtener k éxitos al realizar n ensayos de una población finita de tamaño N.
Ejemplo: Se utiliza para obtener el número de éxitos
en un muestreo sin reemplazamiento de una población finita
de tamaño N. En el siguiente gráfico se muestra la función de probabilidad de una distribución Hipergeométrica basada en una población finita de 100 elementos (N), en la que se seleccionan 20 elementos (n) y se esperan 10 éxitos. 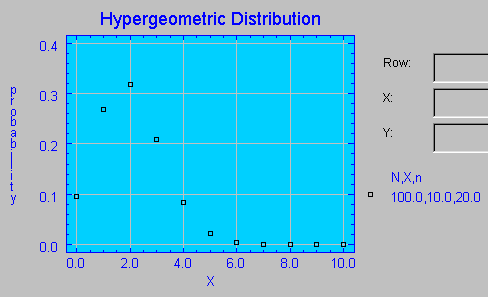 En la dirección http://home.clara.net/sisa/hypergeo.htm se puede acceder a una página con la calculadora que se muestra a continuación, en la que se han introducido los parámetros utilizados en el gráfico anterior para el cálculo de probabilidades no acumuladas basadas en la función de probabilidad de la distribución Hipergeométrica. S.I.S.A. Simple Interactive Statistical Analysis.  Se observa cómo la probabilidad de obtener 4 éxitos en una extracción de 20 elementos sobre 100 es de 0.08410730, sabiendo que la proporción esperada de éxitos es de 10 sobre 100 (0.1). Esta probabilidad obtenida se puede leer de forma aproximada en el gráfico anterior para X=4.
Generaliza la distribución binomial al caso en que la población se divida en k>2 grupos mutuamente exclusivos y exhaustivos. Permite obtener la probabilidad de la ocurrencia de una determinada repartición.
En este caso se cumple que n = x1 + x2 + ... + xk , donde cada xi tiene una probabilidad pi de ocurrencia. Se cumple que ∑pi=1.
También conocida con el nombre de distribución rectangular, se simboliza por medio de U(a,b) y viene determinada por el menor valor posible a que toma la variable y por el mayor valor posible b, siendo b>a. En esta distribución todos los valores comprendidos entre a y b tienen la misma probabilidad de ocurrencia.
Simulación de una variable aleatoria continua: Método de la transformación reciproca Entre otras aplicaciones, la distribución Uniforme U(0,1) se utiliza para generar observaciones que formen una variable aleatoria Y que tenga cualquier función de distribución F(y) continua. Para ello, en primer lugar, se genera un número aleatorio x de la distribución U(0,1). Se resuelve la ecuación F(y)=x, lo que proporciona como solución un valor y* que será el valor de la variable aleatoria simulada. Se repite este proceso tantas veces como se quiera. 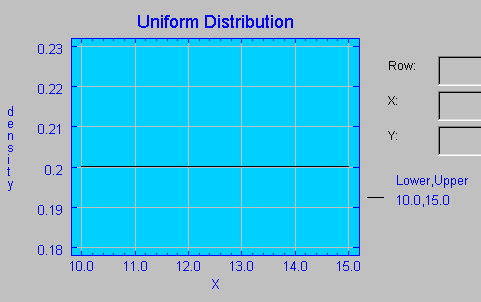
En la dirección http://www.stat.ucla.edu/calculators/cdf/uniform/uniformcalc.phtml encontrará un calculador de la probabilidad acumulada en un valor X situado en una distribución Uniforme (a,b). UCLA Statistics. 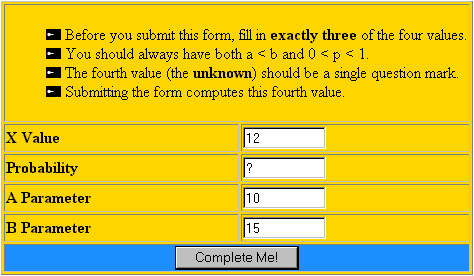 Especificando 3 de los valores proporciona el cuarto, en el que debe escribirse un signo de interrogación. Como ejemplo, si se pretende calcular la probabilidad acumulada en el valor X=12 de una distribución Uniforme (10,15) se obtendría el valor ?=0.4, es decir, Pr(X≤12)=0.4.
Gráfico
de la distribución acumulada.UCLA Statistics.
Se denomina así por el hecho de que la función de densidad tiene una forma triangular, que viene definida de la siguiente manera:
Se denomina triangular cuando viene definida por dos parámetros, que representan el valor mínimo y el valor máximo de la variable. En este caso el triángulo es equilátero. Se denomina triangularG (triangular general), cuando viene dada por tres parámetros, que representan el valor mínimo y el valor máximo de la variable, y el valor del punto en el que el triángulo toma su altura máxima. En este caso el triángulo no es necesariamente equilátero. La función de densidad de la distribución triangularG viene dada por:
Cuando el valor de c sea la media de los dos valores extremos a y b, tendremos la distribución triangular. En el siguiente gráfico se puede ver una distribución triangular (triángulo equilátero de color negro) y una triangularG (triángulo no equilátero de color rojo). 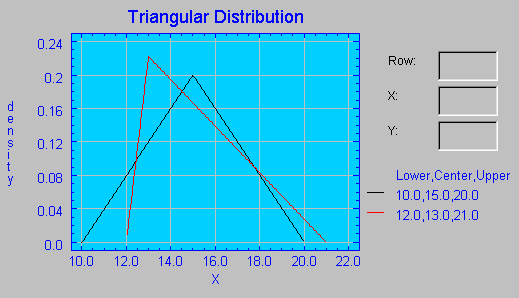
Se dice que una variable X se distribuye de forma log-normal si su logaritmo natural LnX se distribuye normalmente. Se simboliza mediante L(μ , σ) ya que los parámetros de esta distribución son los mismos de los de la distribución normal, μ y σ . Sin embargo, debe quedar claro que μ y σ no son la media y desviación de la distribución log-normal (Ver el apartado de esperanza y variancia de las distribuciones continuas).
Esta distribución es usada para modelizar datos que presentan asimetría positiva. A continuación se proporciona el gráfico que el programa STATLETS realiza al especificar los parámetros 3 y 0.9 para la distribución Lognormal. Creemos que este programa utiliza esta distribución de forma incorrecta ya que usa los parámetros μ y σ como la media y desviación estándar de la distribución, que como hemos dicho anteriormente es incorrecto. 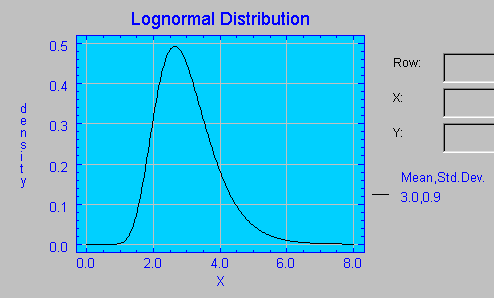 Nuestra creencia en que los cálculos bajo esta distribución no son correctos, viene apoyada en que sus resultados difieren de los obtenidos con otros programas tipo MINITAB o SPSS.
Esta distribución depende de dos parámetros λ y k denominados parámetros de escala y de forma respectivamente. Es decir, al variar k varía la forma de la distribución, mientras que al variar λ sólo varía la escala de la distribución.
Donde la función gamma de p>0, Γ(p), viene dada por:
Si p=1/2 entonces se tiene que Γ(1/2)=√π
Si definimos el valor del parámetro λ en función del parámetro k y del parámetro μ según la expresión λ =k/μ , se tiene que la función de densidad se escribe:
En esta expresión, el parámetro μ
determina la localización de la distribución (μ es la media de la distribución
gamma), y el cociente μ 2/k
determina la forma de la distribución (μ
2/k es la variancia de la distribución gamma). Casos particulares: Si k=1 se tiene la distribución exponencial Esta distribución se ha aplicado a los tiempos de vida de sistemas eléctricos y mecánicos, a la abundancia de especies animales, a períodos de incubación de enfermedades infecciosas, etc.
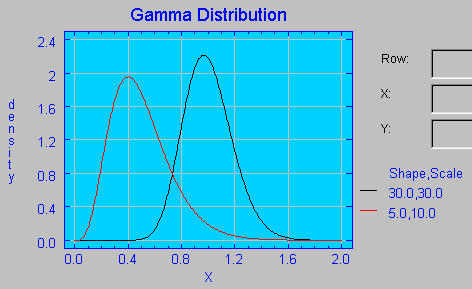
En la dirección http://www.stat.ucla.edu/calculators/cdf/gamma/gammacalc.phtml accederá a un calculador de probabilidades acumuladas basadas la distribución Gamma. En dicha aplicación, especificando 3 de los siguientes valores proporciona el cuarto (en el que debe introducirse un signo de interrogación): valor de X, probabilidad acumulada, parámetro de escala y parámetro de forma. UCLA Statistics.  Como ejemplo, se ha calculado la probabilidad acumulada en el punto X=1 con parámetros de escala y de forma igual a 30, de forma que Pr(X≤1)=0.524283.
Gráfico
de la distribución acumulada.UCLA Statistics.
Esta distribución corresponde a la distribución
Gamma cuando k (parámetro de forma) es un valor entero. Por lo tanto, si tomamos como ejemplo la distribución Erlang con parámetro de forma 15 y parámetro de escala 5 obtendríamos que Pr(X≤3)= 0.534346, valor equivalente en una distribución Gamma con los mismos parámetros. No existirá esa igualdad cuando el parámetro de forma no sea un valor entero.
Esta distribución depende de un parámetro positivo, λ > 0, llamado parámetro de tasa.
Si la función de densidad se escribe en términos de la media μ de la distribución se tiene que:
Se denomina distribución exponencial de dos parámetros cuando se introduce un valor G, por debajo del cual la función de densidad es cero.
Permite estudiar el tiempo transcurrido entre un instante inicial y el momento en que ocurre un determinado suceso. Por ejemplo, la duración de una llamada telefónica, el tiempo transcurrido entre la llegada sucesiva de dos sujetos a un determinado servicio, etc.
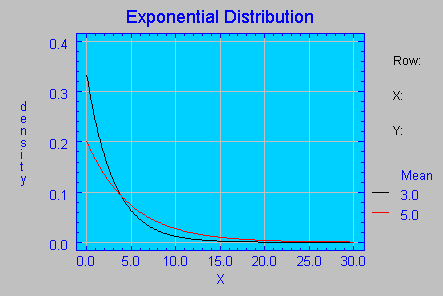
Para el cálculo de probabilidades acumuladas basadas en la función de distribución Exponencial se puede acceder a un calculador ubicado en la siguiente dirección de Internet: http://www.stat.ucla.edu/calculators/cdf/exponential/exponentialcalc.phtml.UCLA Statistics.  Especificando 2 de los valores proporciona el tercero, en el que debe escribirse un signo de interrogación. Como ejemplo, se pretende calcular la probabilidad acumulada en el valor X=5 de una distribución Exponencial con parámetro λ =3. Se obtendría que Pr(X≤5)=0.811124. Igualmente, se podría calcular el valor X por debajo del cual existe una determinada probabilidad acumulada, simplemente introduciendo dicha probabilidad en el campo correspondiente y un signo de interrogación en el campo X value, para posteriormente pulsar el botón Complete Me!.
Gráfico
de la distribución acumulada.UCLA Statistics.
Esta distribución generaliza la distribución exponencial y depende de dos parámetros α y β . El valor de β determina la forma de la distribución mientras que el valor de α determina su escala.
Esta distribución se generaliza a una que depende de tres parámetros, denominada W(α, β, μ) siendo α >0, β >0 y μ≥ 0. El parámetro μ es el valor más pequeño que puede tomar la variable.
La distribución Weibull es una de las pocas distribuciones que puede ser usada para modelizar datos que presentan asimetría negativa.

Distribución Gumbel, de valor extremo o de Gompertz Está definida para todo valor de x, siendo μ un parámetro de localización (moda) y σ >0 un parámetro de escala. Los valores de la variable aleatoria son no negativos, mientras que el dominio de la distribución se mueve en todo el eje real.
En la siguiente figura se muestran dos funciones de densidad Gumbel, una de ellas con parámetro moda 3 y parámetro escala 5, y la otra con parámetros 5 y 10 respectivamente. 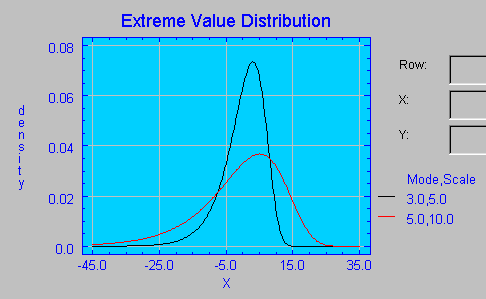
Esta distribución depende de dos parámetros, p (forma) y q (escala), ambos positivos. Se denomina B(p,q).
Donde la función beta B(p,q) viene dada, para p y q positivos, por:
La función beta tiene la siguiente propiedad:
La distribución B(1,1) equivale a la distribución Uniforme U(0,1).

En la dirección http://www.stat.ucla.edu/calculators/cdf/beta/betacalc.phtml tendrá acceso a un calculador de probabilidades acumuladas basadas en dicha distribución. Especificando 3 de los siguientes valores proporciona el cuarto (en el que debe introducirse un signo de interrogación): valor de X, probabilidad acumulada, parámetro p (A Parameter) y parámetro q (B Parameter). UCLA Statistics.  Gráfico
de la distribución acumulada.UCLA Statistics.
Esta distribución depende de dos parámetros, μ y θ . Se denota mediante C(μ , θ).
Donde μ > 0. La distribución es simétrica respecto del valor θ. El valor de x=θ representa la mediana y la moda de la distribución. Se denomina distribución de Cauchy estándar si a una variable X que sigue la distribución de Cauchy le hacemos el cambio de variable Y=(X-θ)/μ , se obtiene la función de densidad de la distribución C(1,0):
En el siguiente gráfico se muestra la función de densidad de una distribución de Cauchy con parámetro μ =25 (Mode) y parámetro θ= 3 (Scale). 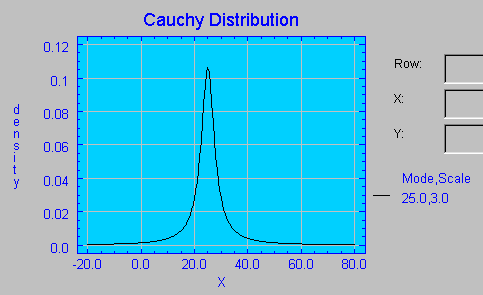 Para calcular probabilidades acumuladas en una distribución de Cauchy puede utilizar el siguiente enlace: http://www.stat.ucla.edu/calculators/cdf/cauchy/cauchycalc.phtml , que accede a una página con la calculadora que se muestra a continuación, en la que se han introducido los parámetros utilizados en el gráfico. UCLA Statistics. 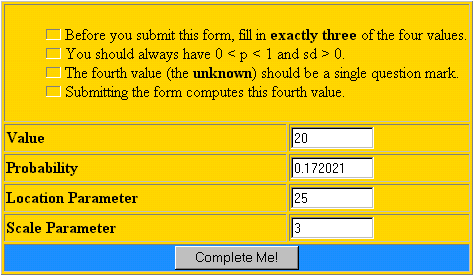 Especificando 3 de los valores proporciona el cuarto, en el que debe escribirse un signo de interrogación. Con los parámetros del gráfico anterior se obtiene que Pr(X≤20)=0.172021.
Gráfico
de la distribución acumulada. UCLA Statistics.
Esta distribución depende de dos parámetros, la media α de la distribución y la desviación estándar β de la distribución. Los valores de la variable aleatoria son no negativos, mientras que el dominio de la distribución se mueve en todo el eje real.
Si se hace el cambio de variable Y=(X-α )/β se obtiene la distribución logística estándar con función de densidad dada por:
A continuación se proporciona un gráfico en
el que se representan dos distribuciones logísticas con
distintos parámetros. 
En la dirección http://www.stat.ucla.edu/calculators/cdf/logistic/logisticcalc.phtml
encontrará un calculador basado en la función de
distribución Logística. Especificando 3 de los
siguientes valores proporciona el cuarto (en el que debe introducirse
un signo de interrogación): valor de X, probabilidad acumulada,
parámetro α (Location Parameter)
y parámetro β (Scale Parameter).
UCLA Statistics. Se ha calculado como ejemplo la probabilidad acumulada hasta el valor X=25 situado en una distribución Logística con parámetro α =30 y parámetro β =5. Como resultado, se obtiene que la probabilidad que el valor X deja a su izquierda es igual a 0.268941, es decir, Pr(X≤25)= 0.268941.
Gráfico
de la distribución acumulada.UCLA Statistics.
También se denomina doble exponencial. Viene determinada en función de dos parámetros, uno de localización L (la media) y otro de escala S, siendo S > 0.
Es una distribución más apuntada que la distribución
normal.
Así lo hacen, por ejemplo, los programas STATLETS y STATGRAPHICS. La función de densidad entonces se escribe como:
A continuación se ofrece la gráfica de la función de densidad de la distribución de Laplace con parámetros 0 y 1. 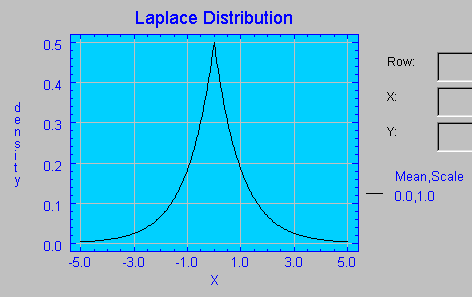
En la dirección http://www.stat.ucla.edu/calculators/cdf/laplace/laplacecalc.phtml encontrará un calculador basado en la función de distribución de Laplace. UCLA Statistics. 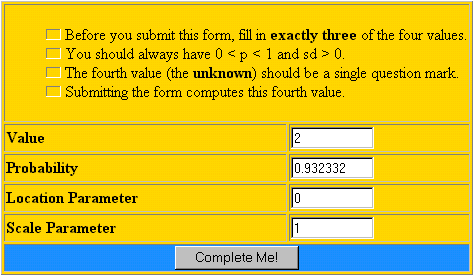 Especificando 3 de los siguientes valores proporciona el cuarto (en el que debe introducirse un signo de interrogación): valor de X, probabilidad acumulada, parámetro media (Location Parameter) y parámetro de escala (Scale Parameter). Como ejemplo, y basándonos en los parámetros del gráfico anterior, se obtiene que Pr(X≤2)= 0.932332.
Gráfico
de la distribución acumulada.UCLA Statistics.
Esta distribución depende de dos parámetros positivos, α y x0. La introdujo Pareto para describir unidades económicas tales como salarios, rentas, etc., y se simboliza mediante Par(α , x0) Permite calcular la probabilidad, por ejemplo, de tener una renta superior a un determinado valor x0.
Si no se indica el segundo parámetro, se entiende que este valor es 1. A continuación se proporciona un gráfico en el que se muestran dos distribuciones de Pareto con distintos parámetros. 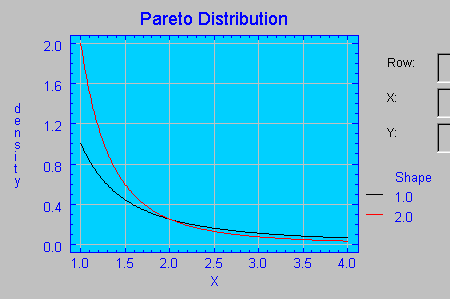
En Internet podemos "bajar" de forma gratuita el programa STATLETS que se encuentra en http://www.statlets.com en su versión no comercial, el cual, entre otras posibilidades que le da los 50 Java applets que contiene, permite obtener una serie de gráficos y de valores para un amplio conjunto de distribuciones. El siguiente gráfico recoge la pantalla de este programa en su apartado de distribuciones, en el que se encuentran los nombres de las 24 distribuciones disponibles. Para llegar a esta pantalla ejecutamos el programa STATLETS y en el menú elegimos Plot | Probability Distributions 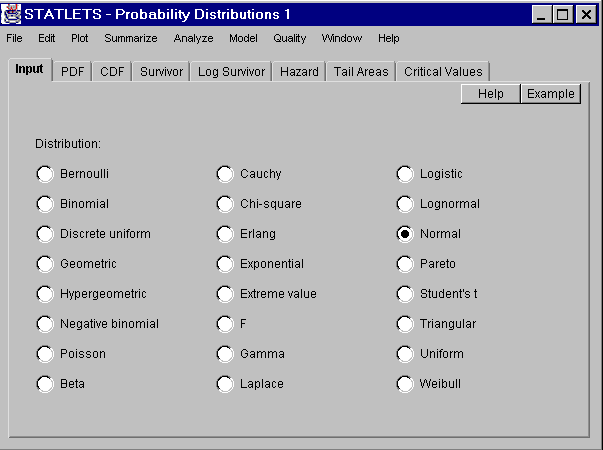
Palmer, Jiménez y Rubí (1999). Tablas estadísticas en Internet I: Cálculo de probabilidades en las distribuciones comunes en el análisis de datos.
Algunas de las distribuciones presentadas no llevan asociadas ninguna dirección de Internet, pero han sido incluidas ya que pueden ser trabajadas por medio del STATLETS.
Uniforme discreta: UD(a,b)
Binomial negativa: BN(r,p)
Geométrica: G(p)
Hipergeométrica: H(N,n,p)
Esperanza y Variancia de las distribuciones continuas
Uniforme: U(a,b)
TriangularG
LogNormal
Gamma: G(λ ,k)
Exponencial: Exp(λ )
Weibull: W(α ,β )
Valor extremo
Beta: B(p,q).
Cauchy: C(μ ,θ )
Ver Aranda y Gómez (1992, p. 145)
Logística
Laplace: L(L,S)
Pareto: Par(α , x0)
Referencias Aranda, J. y Gómez, J. (1992). Fundamentos de estadística para economía y administración de empresas. Barcelona: Ed. P.P.U. Castillo, E. (1978). Introducción a la estadística aplicada. Tomo 1. Santander (editado por el autor). Lindsey, J.K. (1995). Introductory statistics. A modelling approach. Oxford: Clarendon Press. Mendenhall, W., Scheaffer, R. y Wackerly, D (1986). Estadística matemática con aplicaciones. México: Grupo Editorial Iberoamérica. Miller, J. (1997). CUPID: a program for computations with univariate probability distributions. Versión 1.1. Department of Psychology. University of Otago. Dunedin, New Zealand. Palmer, A. (1995). Fundamentos matemáticos para el análisis de datos en Psicología. Palma de Mallorca: Universitat de les Illes Balears. Col.lecció materials didàctics, 3. Palmer, A., Jiménez, R. y Rubí, A. (1999). Tablas estadísticas en Internet I: Cálculo de probabilidades en las distribuciones comunes en el análisis de datos. Publicación electrónica Intersalud.net (Junio 1999), Vol. 1, núm.2, ISSN: 1575-2089. Disponible en: http://areademetodologia.uib.es/articulos/Tablas1/Inicio.htm Walpole, R. y Myers, R. (1992). Probabilidad y estadística. México: Mc Graw-Hill. Tablas Domènech, J.M. (1987). Tablas de estadística. Barcelona: Editorial Herder. Meredith, W. (1971). Manual de tablas estadísticas. México: Ed. Trillas. Palmer, A. (1995). Tablas de estadística. Palma de Mallorca: Universitat de les Illes Balears. Col.lecció materials didàctics, 7. Pearson, E.S. y Hartley, H.O. (eds.)(1954). Biometrika tables for statisticians, Vol.1. Cambridge University Press. Zar, J.H. (1984). Biostatistical analysis (2ªed.). Prentice-Hall. |
||
|
|
Copyright © InterSalud 1999 |
|